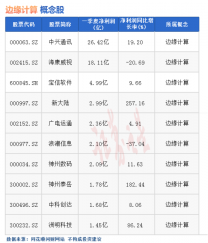
3. 扩展到十六进制
原理还是相同的:直接把十进制中的 10 换成 16 即可:
每一个数位上包括的数字为 0 到 9,A 到 F;
每一个数位上的数,是它右侧数位的 16 倍;
两个数相加时,相同数位上的数相加之和如果大于等于 16,就向前进 1 位,即:满十六进一;
具体来看就是:
从右数第一个位数上的数字代表多少个 1;
从右数第二个位数上的数字代表多少个 16;
从右数第三个位数上的数字代表多少个 256;
从右数第四个位数上的数字代表多少个 4096;
在十六进制中,需要十六个数字来表示 0 到 15 这些数字,0 到 9 比较好处理,但是从 10 到 15,我们就需要找一些记号来表示,于是人们就想到用 A,B,C,D,E,F 这几个字母来分别表示 10 到 15 这个 6 个数字。
十六进制数据,使用后缀字母 H 来表示,有些场合也可以使用前缀 0x 来表示,本质上没有区别。例如:十六进制数字 1A2BH(或者写作 0x1A2B),每一个数位上的权重如图:

换算成十进制数就是 6699(1 * 4096 + 10 * 256 + 2 * 16 + 11 * 1 = 6699)。
4. 扩展到任意进制
原理仍然相同:直接把十进制中的 10 换成目标进制,例如 5 进制:
每一个数位上包括的数字为 0 到 4;
每一个数位上的数,是它右侧数位的 5 倍;
两个数相加时,相同数位上的数相加之和如果大于等于 5,就向前进 1 位,即:满五进一;
具体来看就是:
从右数第一个位数上的数字代表多少个 1;
从右数第二个位数上的数字代表多少个 5;
从右数第三个位数上的数字代表多少个 25;
从右数第四个位数上的数字代表多少个 125;
再看一个图加深印象:

三、从十进制加法到二进制加法
1. 十进制加法
这个就不必多说了,规则只有 2 条:
两个数,相同数位上的数字进行相加;
每一个数位上的相加结果,满十进一;
例如:
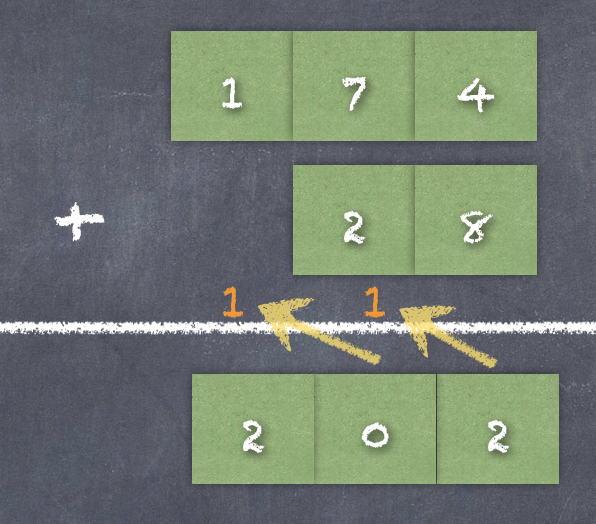
个位上:4 + 8,结果是 12,但是十进制中没有 12 这个数字,因此向左侧的高位进1,个位就剩下:12 - 10 = 2。
十位上:7 + 2,再加上进位 1,结果是 10,但是十进制中没有 10 这个数字,因此向左侧的高位进1,十位变成:10 - 10 = 0。
百位上:1 加上进位 1,结果是 2。
2. 二进制加法

第 0 位:0 + 0 结果为 0;
第 1 位:1 + 0 结果为 1;
第 2 位:1 + 1 结果为 2,但是二进制中没有 2 这个数字,因此需要向左侧的高位进 1,于是第 2 位上就剩下 2 - 2 = 0。
第 3 位:1 + 1 等于 2,再加上进位 1,结果就是 3,但是二进制中没有 3 这个数字,因此需要向左侧的高位进 1,于是第 3 位上就剩下 3 - 2 = 1。
第 4,5,6,7位计算均是如此。