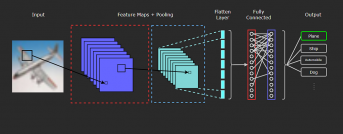
介绍
人工神经网络是受人类神经元工作启发的计算系统。它是深度学习的支柱,在几乎所有领域取得了更大的里程碑,从而带来了我们解决问题的进化。因此,每个有抱负的数据科学家和机器学习工程师都必须对这些神经网络有很好的了解。在本文中,我们将讨论有关人工神经网络 (ANN) 的最重要问题,这有助于让你清楚地了解这些技术,以及数据科学访谈,其中涵盖了从非常基础的层面到复杂概念。
1、感知器是什么意思?
感知器也称为人工神经元,是一种神经网络单元,它执行某些计算以检测特征。它是一个单层神经网络,用作线性分类器,同时处理一组输入数据。由于感知器使用已经标记的分类数据点,因此它是一种监督学习算法。该算法用于使神经元一次一个地学习和处理训练集中的元素。

2、感知器有哪些不同类型?
有两种类型的感知器:
1. 单层感知器
单层感知器只能学习线性可分离的模式。
2. 多层感知器
多层感知器,也称为具有两层或多层的前馈神经网络,具有更高的处理能力。
3、损失函数有什么用?
损失函数用作准确性的度量,以识别我们的神经网络是否在训练数据的帮助下准确地学习了模式。这是通过将训练数据与测试数据进行比较来完成的。因此,损失函数被认为是衡量神经网络性能的主要指标。在深度学习中,性能良好的神经网络在训练发生时始终具有较低的损失函数值。
4、激活函数在神经网络中的作用是什么?
在神经网络中使用激活函数的原因如下:激活函数背后的思想是将非线性引入神经网络,使其能够学习更复杂的函数。没有激活函数,神经网络表现为线性分类器,学习输入数据的线性组合函数。激活函数将输入转换为输出。激活函数负责决定一个神经元是否应该被激活,即是否被激发。为了做出决定,它首先计算加权和,并进一步添加偏差。因此,激活函数的基本目的是将非线性引入神经元的输出。
5、列出神经网络中使用的一些流行的激活函数的名称。
构建深度学习模型时使用的一些流行的激活函数如下:
Sigmoid 函数
双曲正切函数
整流线性单元 (RELU) 函数
Leaky RELU 函数
最大输出函数
指数线性单元 (ELU) 函数

6、成本函数是什么意思?
在构建深度学习模型时,我们的整个目标是最小化成本函数。成本函数解释了神经网络对其给定训练数据和预期输出的表现如何。它可能取决于神经网络参数,例如权重和偏差。总的来说,它提供了神经网络的性能。
7、反向传播是什么意思?
反向传播算法用于训练多层感知器。它将错误信息从网络末端传播到网络内部的所有权重。它允许有效计算梯度或导数。反向传播可以分为以下几个步骤:它可以通过网络转发训练数据的传播以生成输出。它使用目标值和输出值通过考虑输出激活来计算误差导数。它可以反向传播以计算关于前一层输出激活的误差的导数,并继续计算所有隐藏层。它使用先前计算的输出导数和所有隐藏层来计算关于权重的误差导数。它更新权重并重复直到成本函数最小化。
8、如何在神经网络中初始化权重和偏差?
神经网络初始化意味着初始化参数的值,即权重和偏差。偏差可以初始化为零,但我们不能用零初始化权重。权重初始化是神经网络中的关键因素之一,因为错误的权重初始化会阻止神经网络学习模式。相反,良好的权重初始化有助于更快地收敛到全局最小值。根据经验,初始化权重的规则是接近于零但不能太小。
9、为什么权重的零初始化,不是一个好的初始化技巧?
如果我们将神经网络中的权重集初始化为零,那么每一层的所有神经元将在反向传播期间开始产生相同的输出和相同的梯度。结果,神经网络根本无法学习任何东西,因为不同神经元之间没有不对称的来源。因此,我们在初始化神经网络中的权重时添加随机性。
10、解释梯度下降及其类型。
梯度下降是一种优化算法,旨在最小化成本函数或最小化误差。它的主要目标是根据函数的凸性找到函数的局部或全局最小值。这决定了模型应该朝哪个方向减少误差。
梯度下降的三种类型:
小批量梯度下降
随机梯度下降
批量梯度下降

11、解释梯度下降算法中使用的不同步骤。
用于初始化和使用梯度下降算法的五个主要步骤如下:初始化神经网络的偏差和权重。将输入数据通过网络,即输入层。计算预期值和预测值之间的差异或误差。调整值,即神经元中的权重更新以最小化损失函数。我们重复相同的步骤,即多次迭代以确定有效工作的最佳权重。
12、解释术语“数据规范化”。
数据标准化是必不可少的预处理步骤,用于将初始值重新缩放到特定范围。它可以确保反向传播期间更好的收敛。通常,数据归一化将每个数据点归结为减去均值并除以其标准差。由于我们对每一层的输入进行了标准化,因此该技术提高了神经网络的性能和稳定性。
13、神经网络中的前向传播和后向传播有什么区别?
前向传播:输入被送入网络。在每一层中,有一个特定的激活函数,在层之间,有代表神经元连接强度的权重。输入贯穿网络的各个层,最终生成输出。反向传播:误差函数衡量网络输出的准确程度。为了提高输出,必须优化权重。反向传播算法用于确定如何调整各个权重。在梯度下降法期间调整权重。
14、 详细解释不同类型的梯度下降。
随机梯度下降:在随机梯度下降中,使用的批量大小为 1。结果,我们得到了 n 个批次。因此,每次训练样本后都会更新神经网络的权重。
小批量梯度下降:在小批量梯度下降中,批量大小必须介于 1 和训练数据集的大小之间。结果,我们得到了 k 个批次。因此,每次小批量迭代后都会更新神经网络的权重。
批梯度下降:在批梯度下降中,批大小等于训练数据集的大小。因此,神经网络的权重在每个时期之后被更新。
15、 玻尔兹曼机是什么意思?
最基本的深度学习模型之一是玻尔兹曼机,它类似于多层感知器的简化版本。该模型具有一个可见的输入层和一个隐藏层——只是一个两层神经网络,可以随机决定是否应该激活神经元。在玻尔兹曼机中,节点是跨层连接的,但没有同一层的两个节点连接。
16、学习率如何影响神经网络的训练?
在选择学习率来训练神经网络时,我们必须非常谨慎地选择值,原因如下:如果学习率设置得太低,模型的训练将继续非常缓慢,因为我们对权重的变化很小,因为我们的步长由梯度下降方程控制。在达到最小损失点之前需要多次迭代。如果学习率设置得太高,由于步长值较大,权重变化很大,这会导致损失函数出现不良的发散行为。它可能无法收敛(模型可以给出很好的输出)甚至发散(数据太混乱,网络无法训练)。

17、超参数是什么意思?
一旦数据格式正确,我们通常会在神经网络中使用超参数。超参数是一种参数,其值在学习过程开始之前是固定的。它决定了神经网络的训练方式以及网络的结构,其中包括:隐藏单元数学习率epoch 数等。
18、为什么ReLU是最常用的Activation Function?
ReLU(整流线性单元)是神经网络中最常用的激活函数,原因如下:
1. 无梯度消失: RELU 激活函数的导数要么是 0,要么是 1,所以它可能不在 [0,1] 的范围内。因此,几个导数的乘积也将是 0 或 1,由于此属性,反向传播过程中不会出现梯度消失问题。
2. 更快的训练:具有 RELU 的网络往往表现出更好的收敛性能。因此,我们的运行时间要短得多。
3. 稀疏性:对于所有负输入,RELU 生成的输出为 0。这意味着网络中较少的神经元被激发。所以我们在神经网络中有稀疏而有效的激活。
19、解释梯度消失和爆炸的问题。
这些是训练深度神经网络的主要问题。反向传播时,在n个隐藏层的网络中,n个导数将被相乘。如果导数很大,例如,如果使用类似ReLU的激活函数,那么当我们向下传播模型直到最终爆炸时,梯度的值将呈指数增长,这就是爆炸梯度的问题。
相反,如果导数很小,例如,如果使用 Sigmoid 激活函数,那么随着我们在模型中传播,梯度将呈指数下降,直到最终消失,这就是消失梯度问题。
20、优化器是什么意思?
优化器是用于调整神经网络的权重、偏差、学习率等参数以最小化损失函数的算法或方法。这些用于通过最小化函数来解决优化问题。深度学习中最常用的优化器如下:梯度下降随机梯度下降 (SGD)小批量随机梯度下降 (MB-SGD)有动量的SGDNesterov 加速梯度 (NAG)自适应梯度(AdaGrad)AdaDeltaRMSpropAdam
21、为什么深度神经网络比浅神经网络更受欢迎?
除了输入和输出层之外,神经网络还包含隐藏层。浅层神经网络的输入层和输出层之间只有一个隐藏层,而深层神经网络则使用多个层。要逼近任何函数,浅层和深层网络都足够好且有能力,但是当浅层神经网络拟合函数时,它需要学习大量参数。相反,深度网络可以在参数数量有限的情况下更好地拟合函数,因为它们包含多个隐藏层。因此,对于相同的准确度水平,深度的网络在计算和要学习的参数数量方面可以更加强大和高效。关于深度网络的另一件重要事情是它们可以创建深度表示,并且在每一层,网络都会学习新的、更抽象的输入表示。因此,由于其能够处理任何类型的数据建模的能力,现代神经网络已成为首选。

22、过度拟合是每个机器学习从业者面临的最常见问题之一。解释一些避免神经网络过度拟合的方法。
Dropout:这是一种防止神经网络过度拟合的正则化技术。它在训练过程中从神经网络中随机丢弃神经元,相当于训练不同的神经网络。不同的网络会以不同的方式过度拟合,因此 dropout 正则化技术的效果将是减少过度拟合,以便我们的模型有利于预测分析。

提前停止:这种正则化技术更新模型,使其在每次迭代时更好地拟合训练数据。经过一定次数的迭代后,新的迭代会改进模型。然而,在那之后,模型开始过度拟合训练数据。提前停止是指在该点之前停止训练过程。

23、神经网络中Epoch、Batch和Iteration的区别是什么?
Epoch、迭代和批处理是用于处理梯度下降的数据集和算法的不同类型。所有这三种方法,即 epoch、迭代和批量大小,基本上都是根据数据集的大小处理梯度下降的方法。
Epoch:它代表对整个训练数据集(放入训练模型的所有内容)的一次迭代。
Batch:这是指由于计算量大的问题,我们无法一次将整个数据集传递到神经网络中,因此我们将数据集分成几批。
迭代: 让我们有 10,000 张图像作为我们的训练数据集,我们选择批量大小为 200。那么一个 epoch 应该运行(10000/200)次迭代,即 50 次迭代。
24、假设我们有一个感知器,其权重对应于三个输入具有以下值:
W1 = 2;w2 =?4;w3 = 1单元的激活由阶跃函数给出:φ(v) = 1 如果 v≥0否则为 0为以下每个输入模式计算给定感知器的输出值 y:解决方案:要计算每个给定模式的输出值 y,我们必须遵循以下两个步骤:a) 计算加权和:v = Σ i (w i x i )= w i ·x i +w i ·x i +w i ·x ib) 将激活函数应用于 v。
每个输入模式的计算是:
P 1 : v = 2·1?4·0+1·0=2, (2>0), y=φ(2)=1
P 2 : v = 2·0?4·1+1·1=?3, (?3<0), y=φ(?3)=0
P 3 : v = 2·1?4·0+1·1=3, (3>0), y=φ(3)=1
P 4 : v = 2·1?4·1+1·1=?1, (?1<0), y=φ(?1)=0
25、考虑一个前馈神经网络,它具有2个输入(label -1和label** -2),并具有全连接层,而我们有2个隐藏层:
隐藏层 1:标记为 3 和 4 的节点
隐藏层 2:标记为 5 和 6 的节点节点 i 和 j 之间连接的权重由 w ij表示,例如 w24是节点 2 和 4 之间连接的权重。以下列表包含给定网络中使用的所有权重值:w 13=-2, w 35 =1, w 23 = 3, w 45= -1, w 14 = 4, w 36 = -1, w 24 = -1, w 46=1节点 3、4、5 和 6 中的每一个都使用以下激活函数:φ(v) = 1 如果 v≥0 否则 0其中 v 表示节点的加权和。每个输入节点(1 和 2)只能接收二进制值(0 或 1)。计算网络的输出(y 5和y 6),输入模式由(node-1 和node-2 分别为0, 0)给出。
解决方案
要找到网络的输出,需要计算隐藏节点 3 和 4 的加权和:v3 =w13 x1 +w23 x2,v4 =w14 x1 +w24 x2然后使用激活函数 φ 找到隐藏节点的输出:y 3 =φ(v3 ),y4 =φ(v4 )。使用隐藏节点 y3和 y4的输出作为输出层(节点 5 和 6)的输入值,并找到输出节点 5 和 6 的加权和:v5 =w35 y3 +w45 y4,v6 =w36y3 +w46 y4。最后,找到节点5和6的输出(也使用φ):y5=φ(v5),y6=φ(v6)。输出模式将为 (y5 , y6 )。对给定的输入执行此计算 – 输入模式 (0, 0)v3 =?2·0+3·0=0, y3 =φ(0)=1v4 = 4·0?1·0 = 0,y4 =φ(0)= 1v5 =1·1?1·1=0, y5 =φ(0)=1v6 =?1·1+1·1=0, y6 =φ(0)=1因此,对于给定的输入模式,网络的输出是 (1, 1)。
尾注
谢谢阅读!希望你喜欢这些问题,并能够测试你对人工神经网络的了解。