计算每个特征的平均值。这里我们只有两个特征:0和1。s = np.sum(df, axis=0)
mu = s/m
mu
输出:0 14.112226
1 14.997711
dtype: float64
根据上面“公式和过程”部分中描述的公式,让我们计算方差:vr = np.sum((df - mu)**2, axis=0)
variance = vr/m
variance
输出:0 1.832631
1 1.709745
dtype: float64
现在把它做成对角线形状。正如我在概率公式后面的“公式和过程”一节中所解释的,求和符号实际上是方差var_dia = np.diag(variance)
var_dia
输出:array([[1.83263141, 0. ],
[0. , 1.70974533]])
计算概率:k = len(mu)
X = df - mu
p = 1/((2*np.pi)**(k/2)*(np.linalg.det(var_dia)**0.5))* np.exp(-0.5* np.sum(X @ np.linalg.pinv(var_dia) * X,axis=1))
p

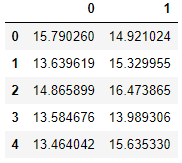
训练部分已经完成。下一步是找出阈值概率。如果概率低于阈值概率,则样本数据为异常数据,但我们需要为我们的特殊情况找出那个阈值。对于这一步,我们使用交叉验证数据和标签。对于你的案例,你只需保留一部分原始数据以进行交叉验证。现在导入交叉验证数据和标签:cvx = pd.read_excel('ex8data1.xlsx', sheet_name='Xval', header=None)
cvx.head()
标签如下:cvy = pd.read_excel('ex8data1.xlsx', sheet_name='y', header=None)
cvy.head()
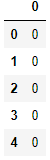
把'cvy'转换成NumPy数组。y = np.array(cvy)
输出:# 数组的一部分
array([[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
这里,y值为0表示这是一个正常的样本,y值为1表示这是一个异常的样本。选择阈值首先让我们再检查一下概率值。p.describe()
输出:count 3.070000e+02
mean 5.905331e-02
std 2.324461e-02
min 1.181209e-23
25% 4.361075e-02
50% 6.510144e-02
75% 7.849532e-02
max 8.986095e-02
dtype: float64




