群卷积
群卷积的目的是通过将特征信道划分为多个不同的组,然后分别对每个组进行卷积,从而减少卷积层中参数的数量,如上图(d)所示。如果我们将特征信道平均分成m组,不改变其他构型,理论上卷积的计算复杂度将会降低到原来的1/m。
深度可分离卷积
上图(e)所示的深度可分离卷积是近年来流行的一种构建轻量级卷积网络的方法,当组数等于信道数时,可以将它看作是群卷积的一个特例[4]。
假设我们有一个带有d个滤波器的卷积层和一个 c 通道的特征图,每个滤波器的大小为 k×k 。对于深度可分卷积,每个 k×k×c 滤波器首先被分割成 c 个片,每个片的大小为 k×k×1 ,然后在每个通道中对滤波器的每个片分别进行卷积。最后,一些 1x1 滤波器用于进行维度转换,以便最终的输出应该具有 d 通道。利用深度可分卷积,将计算复杂度从O(dk^2c)降低到O(ck^2)+O(dc)。该思想最近被应用于目标检测和细粒度分类(Fine-grain classification)。
瓶颈设计
神经网络中的瓶颈层与前一层相比只包含很少的节点,它可以用来学习降维输入的高效数据编码,这在深度自编码中得到了广泛的应用。近年来,瓶颈设计被广泛应用于轻量化网络的设计[5][6]。在这些方法中,一种常见的方法是压缩检测器的输入层,以减少从检测管道开始的计算量[5]。另一种方法是压缩检测引擎的输出,使特征图变薄,使其在后续检测阶段更加高效[6]。
神经结构搜索
近年来,人们对利用神经结构搜索 ( NAS ) 自动设计网络体系结构而不是依赖于专家经验和知识产生了浓厚的兴趣。NAS 已应用于大规模图像分类[7],目标检测[8]和图像分割任务[9]。NAS 最近在设计轻量级网络方面也显示出了很好的结果,其中在搜索过程中考虑了预测精度和计算复杂度的限制[10]。
数值加速技术
我们简要介绍在目标检测中经常使用的两种数值加速技术:1) 频域加速,2) 降阶近似。
频域加速
卷积是目标检测中的一种重要的数值运算形式。由于线性检测器的检测可以看作是特征图与检测器权值之间的窗口内积,因此该过程可以通过卷积来实现。
有很多方法可以加速卷积运算,其中傅里叶变换是一个非常实用的选择,尤其是对于加速那些大的滤波器。频域加速卷积的理论基础是信号处理中的卷积定理,即在合适的条件下,两个信号卷积的傅里叶变换是其傅里叶空间的点乘:

其中,

是傅里叶变换,

是傅里叶反变换,I和W是输入图像和滤波器,*是卷积运算,

是点乘运算。利用快速傅里叶变换 (Fast Fourier Transform,FFT)和快速傅里叶反变换 (Inverse Fast Fourier Transform,IFFT)可以加速上述计算。FFT 和 IFFT 现在经常被用来加速 CNN 模型和一些经典的线性目标检测器,这使得检测速度提高了一个数量级。下图为在频域中加速线性目标检测器的标准传输途径(如 HOG 和 DPM)。

降阶近似
在深度网络中,全连接层的计算本质上是两个矩阵的乘法。当参数矩阵

较大时,检测器的计算量较大。例如在Fast RCNN检测器中,将近一半的前向传递时间用于计算全连接层。降秩近似是一种加速矩阵乘法的方法。它的目的是对矩阵W进行低秩分解:

其中U是由W的前t列左奇异向量构成的

型矩阵,
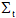
是一个包含W前t个奇异值的

对角矩阵,V是由W的前t行右奇异向量构成的

矩阵。上述过程也称为截断 SVD(Truncated SVD),将参数从
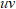
减少到

个,当t远小于

时效果显著。截断 SVD 可以2倍的效率加速 Fast RCNN 检测器。



